Your Complete Guide for Numerical Reasoning Test Formulas

Introduction to our Numerical Reasoning Test Formulas

Numerical Reasoning tests are primarily filled with questions that only require basic maths skills, but there are still some techniques and formulas you must know to quickly and accurately navigate yourself through these tests.

We will cover the following areas: Averages, Percentages, Ratios.

Don't worry there's nothing too complex you will need to know, and you can even keep this resource handy when taking your test (if it's online).

Averages

The average, or 'mean', is found by adding up all the values in the dataset and dividing the total by the number of values.

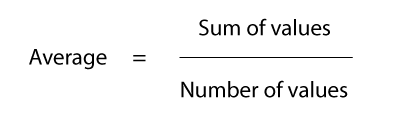
So, now we know that the average is the sum of the values divided by the number of values, let's put this to test in a practise question:

Q: What is the average of the following dataset?

Data set: 4, 27, 60, 90, 133

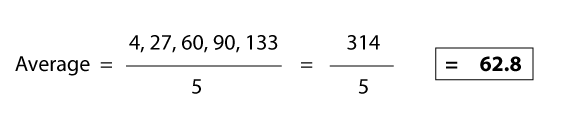
As per above, you will find the correct answer is 62.8.

There are also Weighted Averages

You may be fooled into thinking the question is simply asking you to perform a standard average calculation, but weighted averages are different.

Weighted averages take into account varying levels of importance for numbers in the dataset. The most common ones you will face in a numerical reasoning test will be where you must find the average of maybe to branches of a company or results from a test.

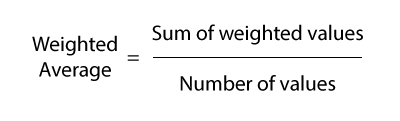
Once again let's put this to practise with an example question:

Q: 15 school children take a test and score an average of 70% between them. The next day 5 more children take the same test and score an average of 80%. What is the combined average score for all these children?

Now it may seem tempting to say the average is 75% because the two averages are 70 and 80. However, this doesn't consider the weight of the averages. There are 15 children who make up the 70% average, compared with 5 generating the 80% average, and so this larger number of values must be taken into account and weighted accordingly.

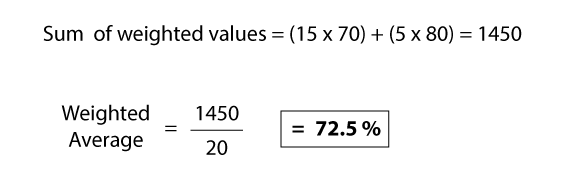
Percentages

Percent literally means ‘per 100’. When we work out percentages, we are presenting a number as parts per hundred.

We calculate percentages by dividing the value by the total, and multiplying the answer by 100.

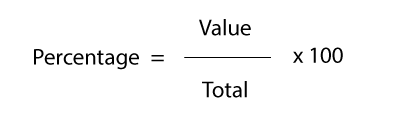
Hopefully, this is easy for you, the real difficulty with percentages arises when we must work out percentage changes and increases/decreases.

Percentage Change (Increase)

So let's go through an example question to see this in practice:

Q: Sales have risen from 130 to 160 in 6 months. What is the percentage change in sales over the 6 months?

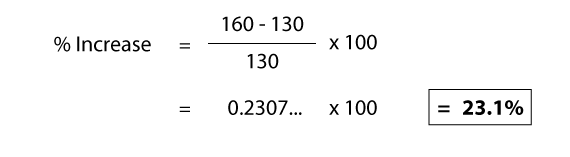
To double check our answer, we can take the original number and multiply it by (new number / original number).

130 x 1.231 = 160.0… as this is the new sales number, we know we are correct.

Percentage Change (Decrease)

Percentage Decreases are very similar to increases. If we use the first percentage change formula above and the answer we get is a negative number, then this tells us that it is in fact a percentage decrease! So if you are unsure about anything, use the formula above first and it will help tell you whether the change is an increase or a decrease.

So let's reverse the previous question:

Q: Sales have fallen from 160 to 130 in 6 months. What is the percentage change?

This will look very similar but this time the top of the equation will be reversed, whereby we subtract 160 from 130.

Then once we plug in the information for the rest of the formula and work it out, we end up with a result of -18.75%.

We can double check this again by multiplying our original number by (new number / original number).

This will result in the calculation: 160 x 0.8125 = 130

Percentage Increase and Decrease

To work out the new value of something after a percentage increase/decrease there is a simple calculation to follow.

The increase and decrease value is worked out where 1 is 100%. Therefore, with a 30% change, the value we would use is 0.3. So we would be either subtracting or adding 0.3 from 1.

Q: This month's sales increased 25% from last month's 400 sales. How many sales were there this month?

As the increase is 25%, this will become 0.25 in our formula. New value = (1+0.25) x 400.

The new sales figures will be 500.

Reverse Percentages

These can commonly be the ones that catch people out, because they know how to calculate the new value after a percentage increase or decrease, but don't know how to calculate the original value after a percentage increase or decrease has occurred.

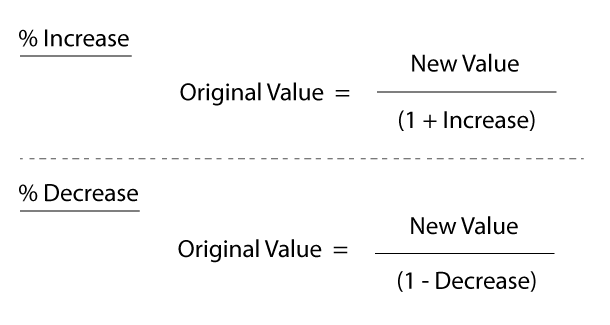
Let's go through a question...

Q: A shirt is on sale at £40 after a 20% reduction. What was the original sale price?

You can see how you can easily be perplexed by this question, trying to work out how to use a standard percentage change formula.

Instead we will use the reverse percentage formula for percentage decreases.

New value = 40 / (1 - 0.20) = 50.

So the original price of the shirt pre-reduction was £50.

Ratios

The last formula we will look at is for ratios.

A ratio tells us how many of one thing there is compared to another.

Use the formula below, where the ratio is Y:Z.

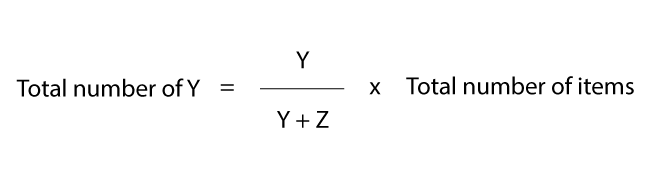
To see this in action, lets use the following question:

Q: There are a total of 80 marbles. The ratio of green marbles to black marbles is 7:3. How many green marbles are there?

Using the formula we can do the following calculation:

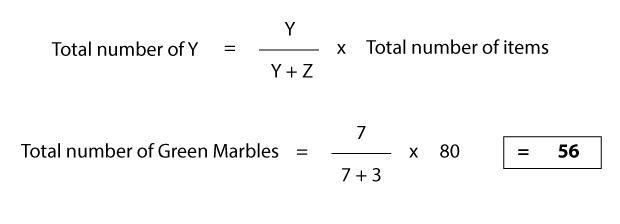
Re-arrange the formula appropriately depending on what values are available to you

And there you have it! That's our top numerical reasoning formula cheat sheet that will help you out of a bind when you take your numerical reasoning test.

Now that you have the all important formulas for numerical reasoning success, it's important that you practise using them.