Our Complete Guide to Psychometric Tests
Including expert advice on what psychometric tests are to how you should best prepare for them.

Updated:
Introduction to psychometric tests
A psychometric test, also known as an aptitude test, is a common part of many modern-day interviews and assessments. Psychometric tests take many forms and are an umbrella term for any assessment that tests one's cognitive ability or personality. They are now more commonly administered online and will consist of a series of questions whereby you must submit your answers within the time limits.
If you haven't yet encountered a psychometric test then you will very likely do so in the future as they are becoming increasingly utilised as an early stage of an assessment application. Recruiting companies like to use them as a means of filtering out large applicant pools to a much slimmer, manageable pool. As a result, many applicants may struggle to ever get past this stage.
It's our mission to help applicants understand the difficulties and nuances involved in psychometric tests and to ultimately assist you in becoming victorious in whatever tests you may be challenged with.
This guide will explain what psychometric tests are, what you should expect of them, and most importantly, how to tackle them.
Page contents:
Jump to:- What is a psychometric test?
- Why use psychometric tests in recruitment?
- Main types of psychometric tests
- What to expect from a psychometric test
- How hard are psychometric tests?
- What tests do specific companies use?
- Feedback and the future of testing
- How to prepare for psychometric tests
- Tips for your psychometric test
- Can you fail a psychometric test?
- Free Psychometric Tests
- Psychometric test FAQs
- Psychometric test resources
Looking to hire?
We recommend Test Partnership for companies seeking reliable hiring tests.

What is a psychometric test and how do they work?
A psychometric test is an objective way to measure the potential ability of candidates to perform well in a job role. Psychometric tests measure a range of skills from cognitive abilities, knowledge to assessing your personality. They are an extremely popular tool in business recruitment, if you are applying for a job (especially graduate schemes) you may have to take some form of psychometric test(s) as a preliminary round of the application process.
The following video features AssessmentDay founder, Oliver Savill, talking about what psychometric tests are and how they work with Psychologists Alan Redman (Criterion Partnership) and Angus McDonald (Realise Potential).

Why are psychometric tests used in recruitment?
Traditionally recruiters studied your CV and qualifications, and made a decision based on an interview.
Extensive research has shown that actually this is a fairly poor way to pick which candidates are going to be best for the job. What's a better way? You guessed it: a psychometric test. In fact, many employers use a combination of interviews, assessments and psychometric tests.
Why do employers use psychometric tests?
There is a strong correlation between test scores and job performance. If you score highly in a psychometric test, the chances are that you are going to perform well in the job. As an employer, this predictive quality makes psychometric tests very attractive.
Add the fact that they can be administered quickly and efficiently on a large scale and you can see why psychometric tests have become the norm, especially for graduate recruitment.
Let's dive a little deeper into some of the key benefits of psychometric tests for recruitment:
- Objectivity - Hiring purely based on interviews and looking over CV's can lead to decisions being made on instinct. Psychometric testing removes this subjective decision-making nature and offers fairness, free of discrimination and bias, as all candidates take one standardised test.
- Accuracy - Psychometric testing can allow a hiring company to assess candidate's abilities to analyse information, problem solve, make informed judgements, whilst also analysing their behavioural tendencies. Access to this data on all applicants allows the hiring company to make quick, scientifically-backed comparisons of candidates to find the most suitable.
- Speed - Even smaller firms receive hundreds to thousands of applicants for open positions and the time that it would take to fairly look through all applicants is far too large. Psychometric testing allows companies to drastically reduce the size of applicant pools down to whatever size is manageable for the organization.
What are the main types of psychometric tests?
The main types of psychometric tests are ability tests and personality questionnaires. There are many forms of ability tests but numerical reasoning and verbal reasoning are the most common.
Check out our information and tests on the following ability tests:
Numerical reasoning and verbal reasoning are two of the most popular tests used to assess a candidate's ability. If you are applying to graduate schemes or know that the application process for your desired job will include psychometric tests, it's very likely that it will include one, or both, of these tests.
So let's take a deeper look into these two popular test types...
Numerical Reasoning
Numerical reasoning tests are the most popular psychometric test, outside of personality profiling, and so it is important that you are adept at handling this sort of test.
Numerical reasoning tests are used to measure a candidate's ability to interpret numerical data. You must be able to analyse and draw conclusions from the data, which could be presented in tables or graphs. Many candidates may fear a numerical reasoning test, believing that the maths involved will be too complex. The tests aren't designed to test the limits of a candidate's mathematical ability, but more to test your ability to use simple mathematical data to solve problems.
Take a look at the following example question for an idea of what to expect:
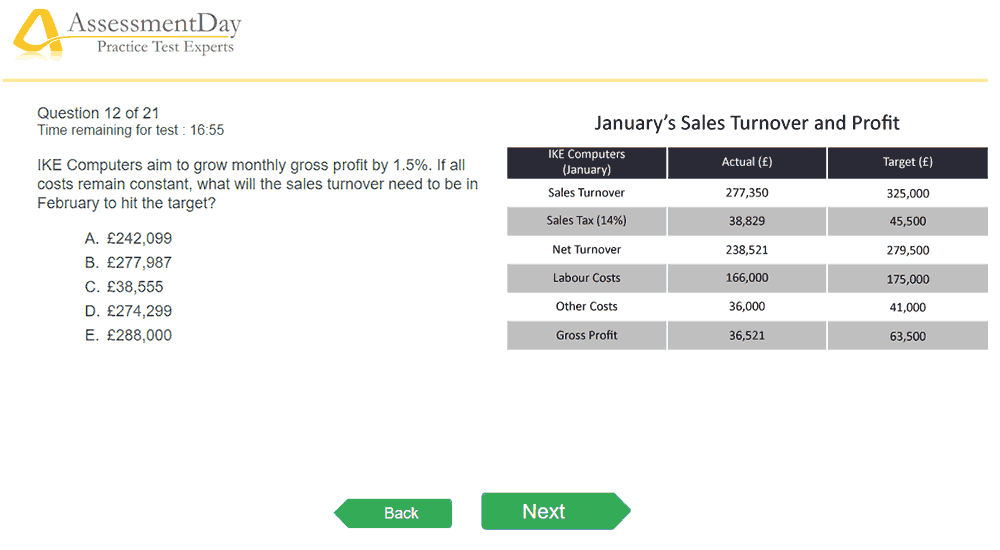
Visit our dedicated numerical reasoning page for more detailed information on what to expect and how to tackle them. We also have practice questions for you to test your ability with.
Start practising quality tests with a free account
Practice makes perfect
- Learn from detailed solutions
- Track your progress
Verbal Reasoning
A verbal reasoning test is used to assess a candidate's ability to comprehend a passage of text. You will, most likely, be presented with a written passage and asked to answer a series of questions with either 'True', 'False' or 'Cannot Say' on the basis of the information given.
You must only use the information that is written in the passage and not use any pre-existing knowledge you may have on the topic as they are not testing this, they're testing your ability to understand text.
Here is an example of a verbal reasoning question:

Visit our verbal reasoning page for further information on verbal reasoning tests along with some practice questions and answers.
What to expect from your psychometric test
The following video once again features Oliver Savill talking about best practices and test standardisation with Psychologists Alan Redman and Angus McDonald.

Psychometric tests are usually timed and in a multiple-choice format. The time constraints will vary from test to test, and it may be that on certain tests you will not be expected to finish all the questions as they were designed to be extremely difficult. So don't panic too much if time is running out and you haven't reached the last few questions.
Try to focus on both speed and accuracy. It's unlikely that the test will be negatively marked (lose marks for incorrect answers) so it may be best to guess an answer for questions you are finding too difficult so you can move on.
If you have a disability that could affect your test performance, you should mention it to the employer beforehand. We have some information on taking psychometric tests with hearing impairments and test anxiety.
What kind of questions are asked in a psychometric test?
Psychometric tests contain questions that are most commonly numerical, verbal and logical. The name of the psychometric test will tell you what sort of questions you will face.
Did You Know
Some psychometric tests use adaptive questioning. This is where the difficulty of your next question may depend on whether you scored correctly on the previous question(s). This is to better understand the candidates ability and to encourage them to finish the test.
How hard are psychometric tests?
The level of difficulty of psychometric tests will vary based on the position you are applying for. Tests for management roles will have either more difficult questions or a higher pass mark compared to entry-level roles.
The difficulty of a test is very subjective - some may find it very hard and other will find it easy. When psychometric tests are used correctly, the candidates that pass would be those that are most likely to be successful at the job they are applying for. This means that how hard you find the psychometric tests will be linked to how hard you will find the day-to-day tasks of the job.
Psychometric tests can seem very difficult to people when they have not taken them before. A lot of the struggles are due to the unfamiliarity of the format and questions. Once someone has practised psychometric tests a lot and is comfortable with the patterns and processes involved, they will find them much easier. Practice is key - we have many test packages available to help you develop your skills.
What tests do specific companies use?
The tests that you are likely to face will depend upon the role and the company you are applying for. However there are core skills that most employers like to test which are verbal, numerical and behavioural.
If you're applying for an accountancy grad scheme with KPMG the tests that will be administered to depict your future job performance will be slightly different to if you were applying for a BBC role. However, like aforementioned, there will be commonalities between the set of tests administered. KPMG will likely test you with numerical, verbal and logical reasoning tests, whereas with the BBC, the application process will include situational judgement tests, personality questionnaires, verbal reasoning and logical reasoning tests.
Visit our Companies Profile Index where we have the tests you will likely face and information on them for 60 of the most popular employers.
It's important to remember that the employer will let you know what the tests are before you take them (this information could also be on their site), and will provide you with ample time (sometimes a week or two) to sit these tests so you will have time to prepare and practice.
Feedback and the future of testing
If the company is following industry-standard best practises, they will provide all candidates with feedback after their test, even to candidates who are unsuccessful. These best practises are guided by the British Psychological Society and all psychometric test administrators should adhere to them (although they are not legally bound to).
Feedback is useful for finding out how to improve your test performance next time. Whilst you will not receive details on each question in your test, you will be given general feedback on your test performance such as:
- how many questions you attempted and how many you got right
- where your score sits relative to a group of other people, expressed as a percentile score
- areas of strength and weakness
Some companies have large volumes of applicants and they decide that they can’t provide individual feedback to everyone, but it is always worth asking. Feedback is useful in understanding where you may have slipped up but most importantly, how you can use feedback to improve future performance.
The following video talks more about feedback, whether psychometric tests work, and the future of testing:

How to prepare for psychometric tests
Tip 1: Study your invitation
Don’t trip at the first hurdle. Before you take your test you should have been given prior notice; this will most likely take the form of an email. Study this invitation and take note of the type of tests they want to assess you on. Once you know the tests you need to take navigate to the appropriate section on our site: such as 'numerical' in order to find information about the test type and practice questions.
If your psychometric test is online, you will be given a deadline by which you must complete the test; typically a week or so. Obviously, make sure you don’t miss the deadline. If you are away or know you won’t be able to complete the online test by the date given, speak to the employer and explain your situation.
This is the best stage at which to ask questions about your psychometric test; there will be plenty of time to explain and help you. This is also the best stage at which to talk to the employer about any special requirements you have, such as adjusting for a disability.
Tip 2: Find the psychometric test publisher
The company you are applying to, or the recruitment agency you are working with, will outsource the design of the psychometric test to a specialist test publisher. Several psychometric test publishers exist and each has slightly different styles. The largest is SHL, but others include Saville Assessment, TalentQ, Cubiks, Criterion Partnership, and Kenexa. Pay careful attention to the online link you get to take your psychometric test and the branding of any test material you get; these will be clues as to which test publisher is behind the psychometric test you are about to sit. As soon as you find out which company has designed the psychometric test, you can go directly to their website and find out even more information about that specific test, such as the time limit, whether negative marking is being used.
Tip 3: Practice, practice, practice
Like most tests, practice can help. There are lots of practice psychometric tests available in books and online, so there is no excuse not to practise. Practising aptitude tests will help you become familiar with the types of questions asked and will reduce your anxiety. If you know what to expect in your test you will be better able to perform your best, instead of being fazed by something new to you. Employers want to measure your true ability and nerves only get in the way of this. So, ensure you practice - we have hundreds of practice material on our site, navigate to our information and practice material for the tests you have to sit and you'll be ready to become an expert.
For personality questionnaires the benefit of practice doesn’t go far beyond helping you to become familiar with the style of questions, since you are who you are and the extent to which you can ‘improve’ your personality is limited. However, for aptitude tests (for example numerical, verbal and inductive tests) practice will allow you to improve your test-taking technique, and generally the score you can achieve. By practising aptitude tests you will typically become faster and more accurate at answering the questions. You will spot time-saving techniques and develop methods for ruling out incorrect answers. The more you practise these types of test the more competent you will become, especially if you haven’t taken a psychometric test before.
Tip 4: Plan your online test session
If your psychometric test is online you will be able to choose where and when you take it. So think about when you work best: is it in the morning, do you work better before or after a meal? Also choose a quiet time when you are least likely to be disturbed. If you are taking your online psychometric test in a shared house, give your housemates advance notice and put a sign on your door asking not to be disturbed. Turn off your phone and any other distractions before your test. The test won't be too long so try and give it all of your attention.
Choose a computer you like to work on; a PC with a large screen and a mouse is better than a small laptop with a touchpad. Another reason to practice psychometric tests beforehand is to establish how and where you personally work best.
Make sure you have everything you need before you start your test: a calculator, a couple of pens, and plenty of rough paper. You want to utilise every second of the test, so it is vital that you don't have to leave the test to find or do something.
PRO TIP
For online numerical reasoning tests you will get to use your own calculator. Make sure you choose one with which you are familiar; perhaps that one you’ve had since your GCSEs for example. The time pressure during psychometric tests is intense, so if you can save a few vital seconds by not having to look down at your calculator to find where the divide button is, then you are giving yourself the best possible chance to perform well.
Another important thing to bear in mind when you take your online test is whether your calculator displays your typing on the screen. For example scientific calculators will display what you’ve typed on a line above the main line of display. This is very useful when you are adding a list of numbers and you need to quickly check where you got to. Or if you miss-key a button this line will show you whether you need to go back one step. Without this feature on your calculator you will have to clear and start the calculation again – not what you need during your psychometric test. If you would like more numerical tips then check out our numerical reasoning test tips.
Join those now working at top companies
Don't settle for 'try again next year'. Let us help you pass employer tests first time.
Try now for free
Test day advice: Tips for during your psychometric test
Tip 5: Read the instructions carefully
This is another way candidates can fail their psychometric test at the first hurdle. Don't assume the instructions, read them! Some tests may require you to click to finish the test and submit your answers before the time limit expires (I, shamefully, have been a victim of this). It will take a few minutes to read the instructions, I know you will be psyched-up and ready to take on the test, but take some time just to make sure you don't end up not following instructions.
How long do you get to complete your test? Sometimes, there is no time limit at all. Is the time limit for the whole test or is it per question? It is a good idea to write down the start time of your test, so that even if you don’t have a stopwatch, or you forget to start it, you always have a way of knowing how much time is remaining in your test.
Is the question asking for one answer, the nearest answer, a list of answers in order, or the odd one out? The style of questions found in psychometric tests varies so make sure you read carefully the instructions each time.
Tip 6: Understand each question
Understanding the question is different from reading it. Perhaps read the question, think about your answer and then re-read the question to check you are about to attempt what is intended. During your psychometric test, it is very easy under the pressure of time to dive head-first into answering a question only to find half-way through that you’ve misunderstood the question.
Things to look out for in aptitude test questions
- Units. Does it ask for the answer in thousands, in seconds, or a different currency?
- How many decimal places does the question ask for? Does the question ask for your answer to the nearest hundred, nearest kg, nearest £?
- Do you definitely have all the information you need to answer the question or it is not possible to say?
Most psychometric tests include answer options called distractors. These are wrong answers which many people mistakenly thought were correct. During psychometric test trials, common mistakes might form these distractor options to disguise the correct answer. It also means that just because you see the answer you’ve arrived at, it doesn’t necessarily mean you’re correct. Re-read the question and ask yourself whether you have understood it correctly.
Careful reading of each question will help you pick up as many marks as possible during your psychometric test.
Tip 7: You probably don't have time to double-check answers
During exams you may be used to double-checking your answers. Whilst this is admirable in some test scenarios, in a psychometric test the time limits are so tight that the time you spend checking an answer is probably better spent answering another next question. Most people don’t get to the end of their psychometric test within the time limit.
There is obviously a balance to be struck with checking answers during your test, and your personal test-taking style will emerge through repeated practice. Rushing through your test to the end is too fast, and double-checking every question is too slow. A good balance might be to pause at the end of each question and look back at the question; does it look right? Have you got the units correct and have you answered the whole question? Then move on. Some tests don’t allow you to go back to previous questions anyway, so make sure you're happy once you move onto the next.
In your psychometric test, it’s better to answer as many questions correctly than to quickly get to the end whilst getting lots wrong.
Tip 8: The speed vs. accuracy debate
Your psychometric test score is not all about how many questions you get right. The results of your aptitude test will include accuracy and speed ratings showing how many of the attempted questions you got right and how quickly you answered those questions.
If you rush through your test you might score highly for speed but low on accuracy. Would a nuclear power company want to hire someone who prioritises speed over accuracy? Different companies place different weighting on the importance of speed and accuracy, so have a think about the type of company you are applying to and what sort of person they are looking for. Don't interpret this advice incorrectly, if you think speed is important for the role you're applying for, don't focus on speed more than the correct answer. A correct answer is always better than an incorrect one. In most tests, the company will be looking for both speed and accuracy.
Tip 9: Learn the art of best-guess estimates
Most psychometric tests are multiple choice. However, this doesn’t mean you should wildly guess answers you’re not sure of. Will you get negatively marked for wrong answers? Probably not, however, if you guess this will bring down your accuracy score and may cause the psychometric test administrator to think negatively of your risky test-taking approach.
Instead of guessing outright, it is sometimes possible to eliminate some of the multiple choice options using your understanding of what the answer should be. This is a useful technique if you’re short of time during your psychometric test. For example, if you can see that the answer will need to be within a ball-park range, or will need to have certain units, you may be able to discount three of the five options and you are on for a 50:50 chance of getting the question right. This is different to guessing.
Tip 10: Don't get your friends to help
With online tests you are free to take the test from home. You might be tempted to think: "will anyone find out if I get someone to help with my test?" Psychometric test publishers are wise to this and put in place measures to detect collaboration and cheating.
Did You Know
If you pass your online (unsupervised) psychometric test, you may well be re-tested under supervised conditions at the employer’s offices to check that your test score really was achieved by you (this isn't as uncommon as you think). Test publishers use tracking software to detect variation between your responses to the online test and your responses to a follow-up supervised test, often conducted at the employer’s office. If your test responses are too dissimilar they will ask some probing questions.
And bear in mind that employers use psychometric testing to establish your fit for a role. If you start a job as a result of a doctored test result, you are probably not right for the role and are likely to become unhappy or stressed, which is in nobody’s interest.
Tip 11: Learn the best use of rough paper
During your test make use of rough paper for your workings. Writing down parts of your working is helpful, but writing down every step will use up precious time. The trick is to find a balance which works best for you; this will develop from repeated practice sessions.
From sitting lots of numerical tests you will get a feel for which are the key stages of a calculation which would be useful to write down, and which numbers you can just leave in your calculator. Also, if your workings are scribbled in so much of a rush that they are meaningless, you will have to spend more time re-doing the calculation, so write down the question number next to your workings.
Can you fail a psychometric test?
Yes, you can fail a psychometric test by not meeting the pass mark. There will be a pass mark set by the employer - the pass mark should be achievable for a lot of candidates, mostly the employer wants to slim down the candidate pool, they are not looking to create a test where only the top 5% will progress.
What to do if you have failed your test
Psychometric Tests are created to challenge candidates - they're designed to be difficult. If you've been unsuccessful after this stage of the application process then don't be too hard on yourself.
Failure is simply the opportunity to begin again, this time more intelligently.Henry Ford
Remember, you've only failed if you give up. You must get back up, dust yourself off, and better prepare yourself to go again. Sometimes all it takes is a bit more practice.
We encourage you to check out all the resources on our site and try our practice tests for free to give you the best chance of reaching those high test performance levels.
Psychometric test FAQs
- Are psychometric tests hard?
- Do people cheat in psychometric tests?
- What is the benefit of psychometric tests?
- What questions are asked in a psychometric test?
Additional psychometric test resources
We have lots of specialised and specific psychometric test advice waiting for you. Simply navigate over to our resources section where you can find all of our test advice, or click on one of the following links you may find useful: